The maths traders in Australia were discussing whether it was possible in a maths trade to offer multiple items in exchange for one in a maths trade. No it's not, it doesn't even nearly work for reasons which are obvious to mathematicians. However I thought about it for a bit, and realised that with the introduction of a pricing mechanism, there can be such a trade. So I borrowed some symbols from the Z Notation (in which I was trained as an undergrad) and wrote this spec:
Let I be the set of items in the trade.
Let U be the set of users in the trade.
Let P be the set of prices, objects that can be summed and are totally ordered.
# every item has an owner, "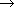 " means total function
" means total function
owns : I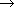 U
U
# if you don't own anything you're not in trade
ran(owns) = U
# some people assign values to some things, "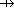 " means partial function
" means partial function
values : U I
I 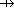 P
P
# For each user u, there is a function vu, which is the values that user places on items
vu = { (i,p) | (u,i)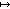 p
p  values }
values }
# and that user at least values the things they own
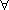 u:U
u:U  owns~
owns~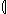 {u}
{u}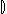
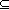 dom(vu)
dom(vu)
# Then a valid solution to the trade is an assignment of items to users
s : I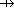 U
U
# the items received by u are
ru = s~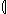 {u}
{u}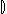
# the items sent by u are
su = owns~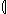 {u}
{u}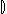
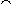 ran(s)
ran(s)
# such that nothing is assigned to the person it came from
s owns =
owns = 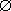
# and everyone gets a bargain, by their own personal pricing rules
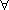 u:ran(s)
u:ran(s)  Σ (i
Σ (i  ru) vu(i)
ru) vu(i)  Σ (i
Σ (i  su) vu(i)
su) vu(i)
# For a solution to be useful, it must be non-trivial:
s
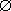
# and furthermore, we would like to restrict ourselves to minimal solutions so as to not make offered trades incomprehensibly complex, so if t is a solution, then t is not a subset of s (can't find the right symbols to write that!)
Let I be the set of items in the trade.
Let U be the set of users in the trade.
Let P be the set of prices, objects that can be summed and are totally ordered.
# every item has an owner, "
owns : I
# if you don't own anything you're not in trade
ran(owns) = U
# some people assign values to some things, "
values : U
# For each user u, there is a function vu, which is the values that user places on items
vu = { (i,p) | (u,i)
# and that user at least values the things they own
# Then a valid solution to the trade is an assignment of items to users
s : I
# the items received by u are
ru = s~
# the items sent by u are
su = owns~
# such that nothing is assigned to the person it came from
s
# and everyone gets a bargain, by their own personal pricing rules
# For a solution to be useful, it must be non-trivial:
s
# and furthermore, we would like to restrict ourselves to minimal solutions so as to not make offered trades incomprehensibly complex, so if t is a solution, then t is not a subset of s (can't find the right symbols to write that!)
It occurs to me that blogspot is maybe not the ideal medium for writing specifications.
4 comments:
We tried an experimental trade like that once: http://www.boardgamegeek.com/thread/377422/extended-value-loops-trade-discussion-thread
This was with only limited software support, and with the results mostly being calculated by hand.
I think the "minimal solution" criterion would rule out a big trade that was the union of two smaller disjoint trades, which probably isn't what you want. If there was another quality metric for judging the goodness of a solution (such as total value gained or # of users trading) then the minimal solution criterion might apply to solutions with the same score on the quality metric.
The BGG thread is here:
http://boardgamegeek.com/thread/748121/for-maths-geeks-only-the-even-more-complicated-tha
If we were to run this sort of trade as an event, then finding the biggest solution is required. If we were to run it as an on-going process, the smallest solution is sufficient, as we can then run it again. In any case, if we want a big solution we can find a small solution, remove those items from the trade, and find a solution on the remainder. It might not be the best solution, but I think any solution will be handy for us beginners.
You're such a dork.
Post a Comment