The maths traders in Australia were discussing whether it was possible in a maths trade to offer multiple items in exchange for one in a maths trade. No it's not, it doesn't even nearly work for reasons which are obvious to mathematicians. However I thought about it for a bit, and realised that with the introduction of a pricing mechanism, there can be such a trade. So I borrowed some symbols from the Z Notation (in which I was trained as an undergrad) and wrote this spec:
Let I be the set of items in the trade.
Let U be the set of users in the trade.
Let P be the set of prices, objects that can be summed and are totally ordered.
# every item has an owner, "
" means total function
owns : I U
# if you don't own anything you're not in trade
ran(owns) = U
# some people assign values to some things, "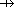
" means partial function
values : U
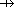I P
# For each user u, there is a function vu, which is the values that user places on items
vu = { (i,p) | (u,i)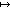
p 
values }
# and that user at least values the things they own
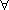u:U 
owns~
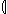{u}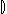
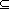dom(vu)
# Then a valid solution to the trade is an assignment of items to users
s : I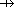 U
# the items received by u are
ru = s~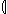{u}
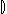
# the items sent by u are
su = owns~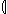{u}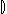 
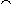ran(s)
# such that nothing is assigned to the person it came from
s
owns =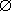 
# and everyone gets a bargain, by their own personal pricing rules
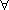u:ran(s) Σ (i ru) vu(i) 
Σ (i su) vu(i)
# For a solution to be useful, it must be non-trivial:
s
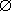
# and furthermore, we would like to restrict ourselves to minimal solutions so as to not make offered trades incomprehensibly complex, so if t is a solution, then t is not a subset of s (can't find the right symbols to write that!)
Let I be the set of items in the trade.
Let U be the set of users in the trade.
Let P be the set of prices, objects that can be summed and are totally ordered.
# every item has an owner, "
" means total functionowns : I
U# if you don't own anything you're not in trade
ran(owns) = U
# some people assign values to some things, "
" means partial functionvalues : U
I P# For each user u, there is a function vu, which is the values that user places on items
vu = { (i,p) | (u,i)
p values }# and that user at least values the things they own
u:U owns~{u} dom(vu)# Then a valid solution to the trade is an assignment of items to users
s : I
U# the items received by u are
ru = s~
{u}# the items sent by u are
su = owns~
{u} ran(s)# such that nothing is assigned to the person it came from
s
owns = # and everyone gets a bargain, by their own personal pricing rules
u:ran(s) Σ (i ru) vu(i) Σ (i su) vu(i)# For a solution to be useful, it must be non-trivial:
s
# and furthermore, we would like to restrict ourselves to minimal solutions so as to not make offered trades incomprehensibly complex, so if t is a solution, then t is not a subset of s (can't find the right symbols to write that!)
It occurs to me that blogspot is maybe not the ideal medium for writing specifications.
